Plantlet The Blogging Platform of Department of Botany, University of Dhaka
We can test the significance of the two sample means by using a t-test. However, in cases where there are more than two samples, it is done by Analysis of Variance (ANOVA). This method is carried out by comparing sample variances using Variance Ratio Test or F test. So at first, let’s learn about the F test which is discussed below:
Variance Ratio Test (F test)
The variance ratio test was first conducted and named after a British statistician called Ronald Aylmer Fisher (17 February 1890 – 29 July 1962). It is any statistical test in which the test statistic has an F-distribution under the null hypothesis. It is most often used when comparing statistical models that have been fitted to a data set, in order to identify the model that best fits the population from which the data were sampled. The value of F is equal to the ratio of variance.
F= Estimate variance between groups ( including treatment effects)/ Estimate variance within groups (excluding treatment effects)
In ANOVA the F test is determined as the final goal that indicates the presence or absence of a significant difference between more than two samples. In the context of ANOVA, the sample variances are called mean squares, or MS values.
Analysis of Variance (ANOVA)
General logic and basic formulas for the hypothesis testing procedure known as analysis of variance (ANOVA). The purpose of ANOVA is much the same as the t-tests. The goal is to determine whether the mean differences that are obtained for sample data are sufficiently large to justify the conclusion that there are meaningful differences between the populations from which the samples were obtained.
There are two methods of ANOVA depending on the condition of samples in which they are grouped.
Best safe and secure cloud storage with password protection
Get Envato Elements, Prime Video, Hotstar and Netflix For Free
Best Money Earning Website 100$ Day
#1 Top ranking article submission website
One-way classification of Variance
If the analysis concerns with testing the difference between two sets of groups without any further categorization according to the other factors concerned, we use one-way ANOVA test. Steps of finding F value in ANOVA is given with examples-
Example- The table is given where it shows a record of the number of new leaves observed under different concentrations of hormone given.
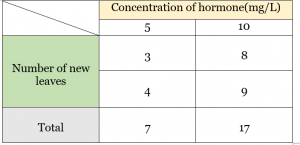
Step1: Write null hypothesis. For example here, it can be stated as “there is no significant difference/ variation among the treatments (different concentration of hormones)”
Step2: Calculate sum of square (Total SS) using the formula- ∑x2 − (∑x) 2 ⁄ n [where (∑x) 2 ⁄ n is the correction factor and “n” is the number of observed samples]
here, Total SS = (32+ 4 2+ 82 +92)− (7+17)2/4
= 170− 144
= 26.
Step3: Calculate Treatment Sum of square using formula- (total of 1st treatment)2/n + …..+(total of last treatment)2/n − (∑x) 2 ⁄ n [where n is the number of observation under one treatment]
here, Treatment SS = (72/2 + 172/2) − (7+17) 2 ⁄ 4
= 169 − 144
= 25.
Step4: Calculate Residual Sum of square using formula – Residual SS= Total SS− Treatment SS
here, Residual SS= 26 − 25 = 1
Step5 : Calculate degrees of freedom (df) for total, treatment, and residual. For total and treatment, it is n−1 and for residual, it is total degrees of freedom− treatment degrees of freedom.
here, treatment df= 2−1 = 1 and
residual df= (4−1) − (2−1)= 2
Step6: Calculate mean square for treatment and residual using formula- Mean square = Sum of square/degrees of freedom.
here, Treatment mean square = 25/1 = 25
and Residual mean square = 1/2 = 0.5
Step7: Calculate variance ratio or F value using the formula – Mean square of treatment/ Mean square of Residual.
Step8: Draw ANOVA table including all the headlines below-
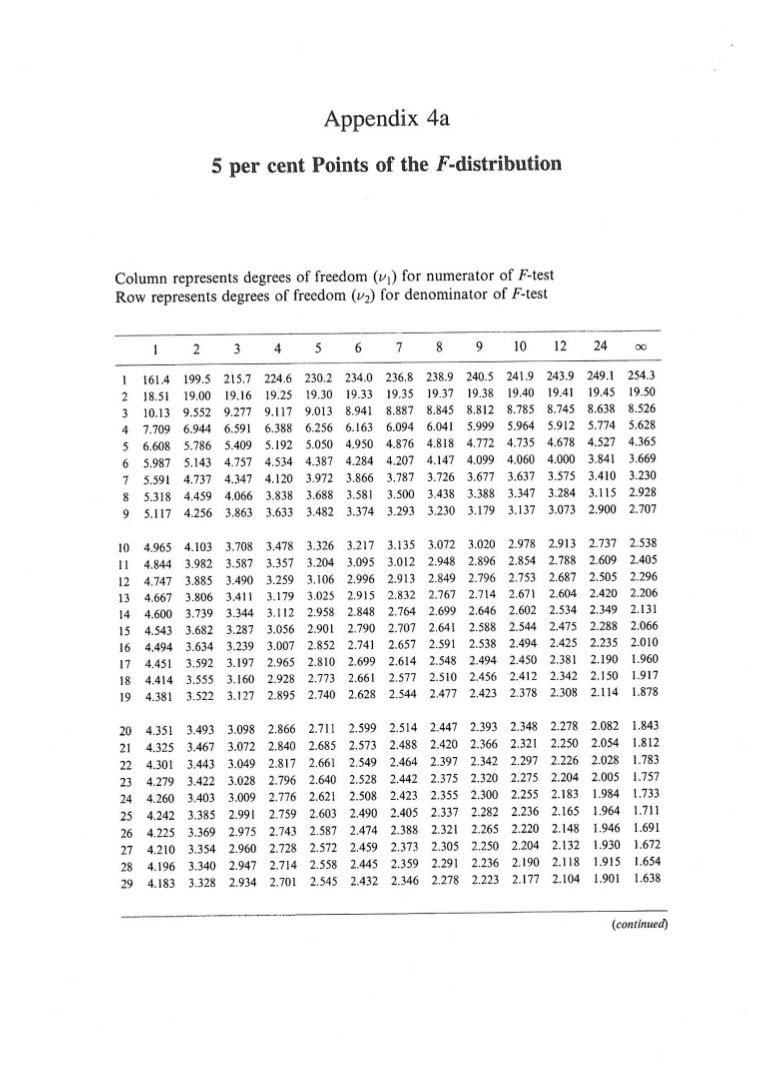
Step9: Compare the calculated F value with that of the F distribution table and comment. If the calculated value is greater than the tabulated value, the null hypothesis is rejected. Thus there is a significant difference in the treatment. If it’s small, vise versa.
Two-way classification of variance
If the analysis is concerns with testing the difference between two sets of groups with further categorization according to two or more factors concerned we use two way ANOVA test. The steps for finding F value in 2 way ANOVA is quite different as in the one way as we have to calculate the treatment sum of square values for treatment and factors separately. So there will be more than one treatment value.
A simplified table is given as an example-
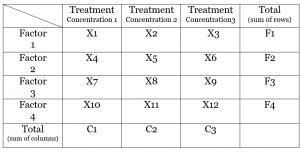
Step1 and 2 are the same as in one-way ANOVA.
Step3: Calculate Treatment Sum of square for both treatments applied and factors using formula- (total of 1st treatment)2/n + …..+(total of last treatment)2/n − (∑x) 2 ⁄ n.
here, Treatment sum of square for treatments (concentration) = (C1)2/n + (C2)2/n + (C3)2/n − (∑x) 2 ⁄ n
and Treatment sum of square for factors = (F1)2/n + (F2)2/n + (F3)2/n + (F4)2/n − (∑x) 2 ⁄ n
Step4: Calculate Residual Sum of square using formula- Residual SS = Total SS − (Treatment SS + Factor SS)
Step5: Calculate degrees of freedom for Total, Treatment, Factor, and Residual as same way done in one way ANOVA
Step6: Calculate Mean square for 2 Treatment Sum of squares for different treatments (concentration) and factor and for residual Sum of squares, using formula- Mean square = Sum of square/degrees of freedom.
Step 7: Calculate variance ratio or F value for both Mean square values.
here, F value for treatments (concentration)= mean square of treatment (concentration)/ mean square of residual
and F value for factors= mean square of factors/ mean square of residual
Step8: Draw ANOVA table including all the headlines below-
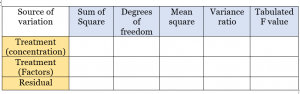
Step9: Compare the calculated F value with that of the F distribution table and comment. If the calculated value is greater than the tabulated value, the null hypothesis is rejected. Thus there is a significant difference in the treatment. If it’s small, vise versa.
F distribution table is given below. We will record the intercept value of horizontal (degrees of freedom for treatment) and vertical (degrees of freedom for residual) as tabulated F value.
Reference
- slides from One way ANOVA, Two way ANOVA, F test by Prof. Rakha Hari Sarker.
- Mahajan’s Methods in Biostatistics for medical students and research workers 9th edition (page-212-217)
