There are various methods to measure the central value of an observation. For instance, average, mean, median, mode, etc.
Average
The average value of a characteristic is the one central value around which all other observations are distributed. In any large series, nearly 50% of observations lie above the central value whereas the other 50% lie below the central value. It indicates how the values lie close to the center.
**Average is the measure that indicates the central tendency or concentration of all other observations around the central value.
There are three types of averages or measures of central position or central tendency -mean, median, and mode.
Best safe and secure cloud storage with password protection
Get Envato Elements, Prime Video, Hotstar and Netflix For Free
Best Money Earning Website 100$ Day
#1 Top ranking article submission website
Mean
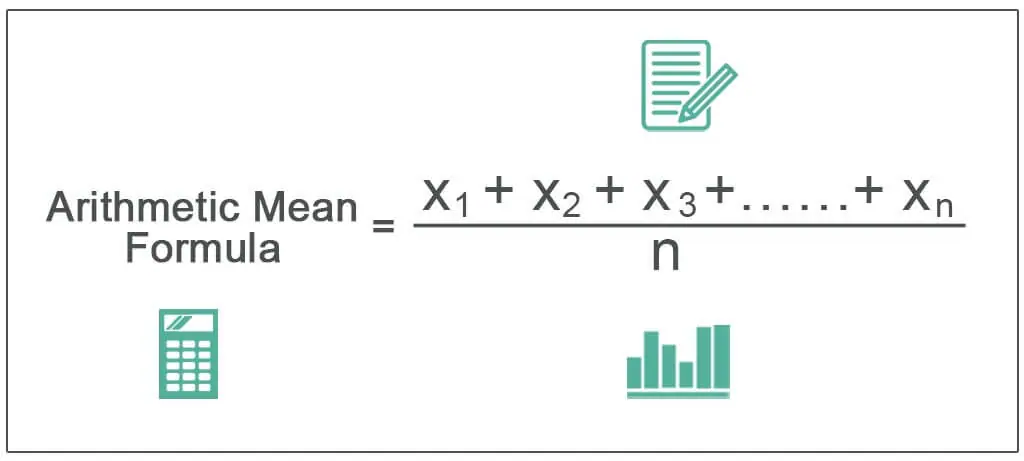
This is an arithmetic average of a collection of values. It is the sum of observations divided by the number of observations.
Let,the observations are x1,x2,x3,….
Mean=∑x/n (n=number of observations)
Mean in case of continuous series:
| Number of organisms | frequency(f) | midpoint(m) | f×m |
| 5-9 | 3 | 7 | 21 |
| 10-14 | 5 | 12 | 60 |
| 15-19 | 6 | 17 | 102 |
| 20-24 | 4 | 22 | 88 |
| 25-29 | 3 | 27 | 81 |
| ∑f=21 | ∑fm=352 |
x¯=∑fm/∑f=352/21=16.76
Median
When all the observations of a variable one arranged in either ascending or descending order, the middle observation is known as the median.
The median is a locational average & it is that value that divides the series into two equal shares in a series of observations. The median equally divides the number of items of observations.

With an even number of observations
The Median will be the average of two values according to the following formula.
when,n=10
n/2=10/2=5th
(n+2)/2=(10+2)/2=6th, Here median will be the average of 5th & 6th value of the series.
Example:4,6,7,8,8,9,11,12,12,14 Here,5th value=8 & 6th value=9
Now,median=(8+9)/2=17/2=8.5
With odd number of observations
Number of nodules/root:7,6,9,8,9,10,6,7,10
Arranged in ascending order:6,6,7,7,8,9,9,10,10
Median=(n+1)/2=(9+1)/2=5th value=8
Median in case of classified data
|
Time (Sec) Class Interval |
Frequency | Cumulative Frequency |
| 30-35 | 3 | 3 |
| 36-41 | 10 | 13 |
| 42-47 | 18 | 31 |
| 48-53 | 25 | 56 |
| 54-59 | 8 | 64 |
| 60-65 | 6 | 70 |
| ∑n=70 |
Median=L+{(n/2-Fc)/fm}×h=48+{(70/2-31)/25}×6=48.96
L= lower value of the highly frequent class (48-53)
n=number of observations [n=70],[2f=70]
Fc=cumulative value of the previous class of the median class [Fc=31]
fm= frequency of median class
h=class interval[h=6]
Mode
This is the most frequently occurring observation in a series.
Mode is the type of average that refers to the most common or most regularly occurring value in a series of data.
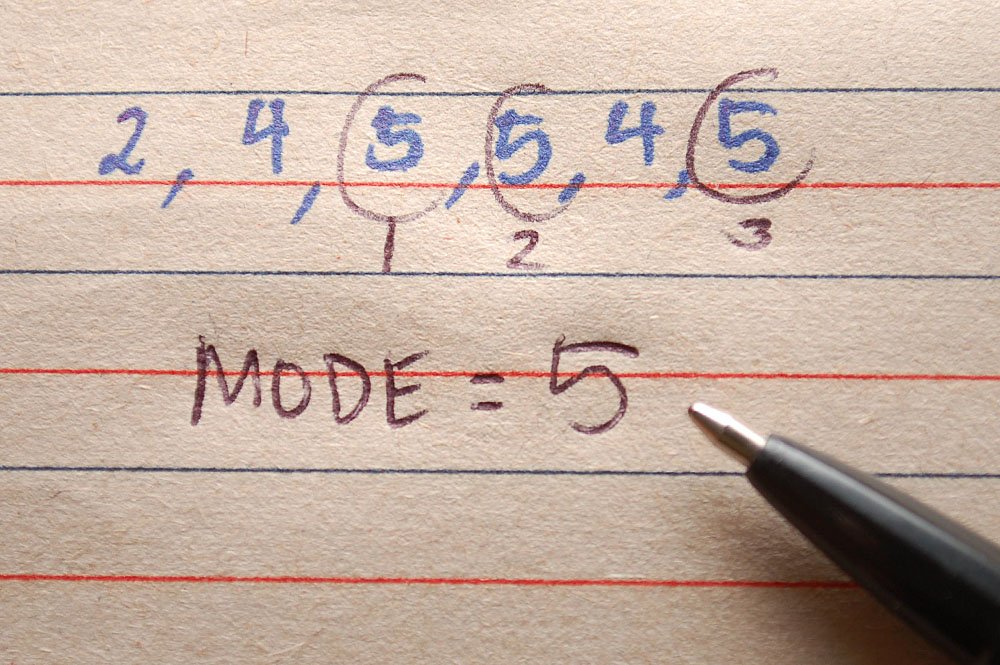
Calculation of mode from classified data
| Class | Frequency |
| 31-40 | 4 |
| 41-50 | 6 |
| 51-60 | 8 |
| 61-70 | 12 |
| 71-80 | 9 |
| 81-90 | 7 |
| 91-100 | 4 |
Mode=L+{f1/(f1+f2)}×h=61+{4/(4+3)}×10=61+0.57×9=66.71
Here,
L=lower value of the modal class=61
f1=frequency of the modal class – frequency of the previous class=12-8=4
f2=frequency of the modal class – frequency of the next class=12-9=3
h=class interval=10
**Out of three measures of central tendency mean is better and utilized more often because it uses all the observations in the data and is further used in the tests of significance
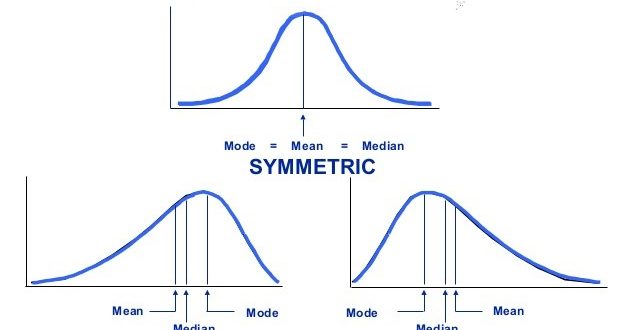
Symmetrical Distribution
Symmetrical distribution is a distribution in which the values of variables occur at regular frequencies, and the mean, median, and mode occur at the same point. Unlike asymmetrical distribution, symmetrical distribution does not skew.
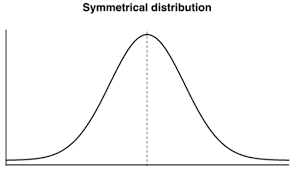
**In short, the distributions in which both sides are the same(mirror image) about the middle ordinate is called symmetrical distribution.
Asymmetrical Distribution
Asymmetrical distribution is a distribution in which the values of variables occur at irregular frequencies and the mean, median, and mode occur at different points. An asymmetric distribution exhibits skewness.

Skewed Distribution
Some distributions are steep on one side and have a long tail on the other side. This characteristic of a distribution is called skewness.
If the tail is on the right side the distribution is said to be skewed right. This type of skewness is called positive skewness.
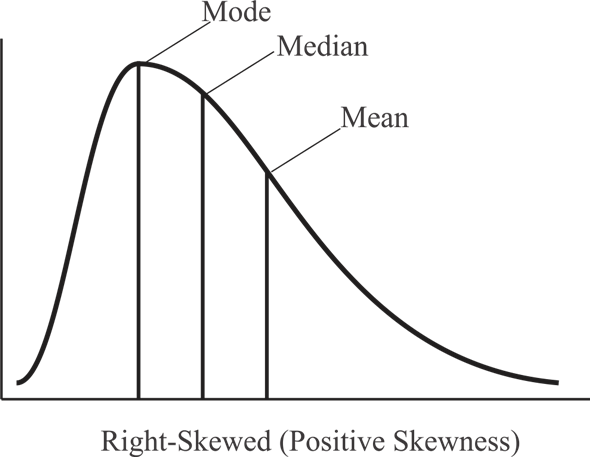
**Biological phenomena are very commonly skewed right.
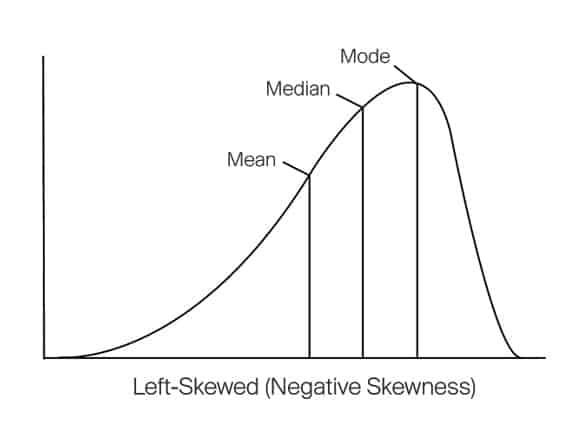
If the tail is on the left side, the distribution is said to be skewed left. This type of skewness is called negative skewness.
**Skewness is a measure of symmetry, or to say more certainly, the lack of symmetry.
Kurtosis
Similar to skewness, kurtosis is a statistical measure that is used to describe the distribution.
Kurtosis is a measure of whether or not the data are heavy-tailed or light-tailed relative to a normal distribution. That is, data sets with high kurtosis tend to own heavy tails or outliers. Data sets with low kurtosis tend to own light tails or lack of outliers.

**Kurtosis=3 depicts the normal distribution
Outlier
In statistics, an outlier is a data point that differs considerably from other observations. An outlier may be due to variability in the measurement or it may suggest experimental error; the latter are generally excluded from the data set. An outlier can cause serious issues in statistical analyses.
Q&A
1. Which of the following data sets has a median of 3?
(A) 3, 3, 3, 3, 3
(B) 2, 5, 3, 1, 1
(C) 1, 2, 3, 4, 5
(D) 1, 2, 4, 4, 4
(E) Choices (A) and (C)
2. To the nearest tenth, what is the mean of the following data set? 14, 14, 15, 16, 28, 28, 32, 35, 37, 38
3. To the nearest tenth, what is the mean of the following data set? 15, 25, 35, 45, 50, 60, 70, 72, 100
4. To the nearest tenth, what is the mean of the following data set? 0.8, 1.8, 2.3, 4.5, 4.8, 16.1, 22.3
5. To the nearest thousandth, what is the mean of the following data set? 0.003, 0.045, 0.58, 0.687, 1.25, 10.38, 11.252, 12.001
6. To the nearest tenth, what is the median of the following data set? 6, 12, 22, 18, 16, 4, 20, 5, 15
7. To the nearest tenth, what is the median of the following data set? 18, 21, 17, 18, 16, 15.5, 12, 17, 10, 21, 17
8. To the nearest tenth, what is the median of the following data set? 14, 2, 21, 7, 30, 10, 1, 15, 6, 8
9. To the nearest hundredth, what is the median of the following data set? 25.2, 0.25, 8.2, 1.22, 0.001, 0.1, 6.85, 13.2
10. Compare the mean and median of a data set that has a distribution that is skewed right.
11. Compare the mean and median of a data set that has a distribution that is skewed left.
12. Compare the mean and the median of a data set that has a symmetrical distribution.
13. Which measure of center is most resistant to (or least affected by) outliers?
1. Ans) E. Choices (A) and (C) (3, 3, 3, 3, 3; 1, 2, 3, 4, 5)
To find the median, put the data in order from lowest to highest, and find the value in the middle. It doesn’t matter how many times a number is repeated. In this case, the data sets 3, 3, 3, 3, 3 and 1, 2, 3, 4, 5 each have a median of 3.
2. Ans) 25.7
Use the formula,
¯x=∑x/n
where ̄x is the mean, ∑ represents the sum of the data values, and n is the number of values in the data set. In this case, x = 14 + 14 + 15 + 16 + 28 + 28 + 32 + 35 + 37 + 38 = 257, and n = 10. So the mean is 257 10 =25.
3. Ans) 52.4
Use the formula for calculating the mean
¯x=∑x/n
where ̄x is the mean, ∑ represents the sum of the data values, and n is the number of values in the data set. In this case, x = 15 + 25 + 35 + 45 + 50 + 60 + 70 + 72 + 100 = 472, and n = 9. So the mean is 472 9 =52.4444
The question asks for the nearest tenth, so you round to 52.4.
4. Ans) 7.5
Use the formula for calculating the mean
¯x=∑x/n
where ̄x is the mean, ∑ represents the sum of the data values, and n is the number of values in the data set. In this case, x = 0.8 + 1.8 + 2.3 + 4.5 + 4.8 + 16.1 + 22.3 = 52.6, and n = 7. So the mean is 52.6 7 =7.5143
The question asks for the nearest tenth, so you round to 7.5.
5. Ans) 4.525
Use the formula for calculating the mean
¯x=∑x/n
where ̄x is the mean, ∑ represents the sum of the data values, and n is the number of values in the data set. In this case, x = 0.003 + 0.045 + 0.58 + 0.687 + 1.25 + 10.38 + 11.252 + 12.001 = 36.198, and n = 8. So the mean is 36.198 8 =4.52475
The question asks for the nearest thousandth, so you round to 4.525.
6. Ans) 15.0
To find the median, put the numbers in order from smallest to largest: 4, 5, 6, 12, 15, 16, 18, 20, 22 Because this data set has an odd number of values (nine), the median is simply the middle number in the data set: 15.
7. Ans) 17.0
To find the median, put the numbers in order from smallest to largest: 10, 12, 15.5, 16, 17, 17, 17, 18, 18, 21, 21 Because this data set has an odd number of values (11), the median is simply the middle number in the data set: 17.
8. Ans) 9.0
To find the median, put the numbers in order from smallest to largest: 1, 2, 6, 7, 8, 10, 14, 15, 21, 30 Because this data set has an even number of values (ten), the median is the average of the two middle numbers: 8+10/2 =9.0
9. Ans) 4.04
To find the median, put the numbers in order from smallest to largest. 0.001, 0.1, 0.25, 1.22, 6.85, 8.2, 13.2, 25.2 Because this data set has an even number of values (eight), the median is the average of the two middle numbers: 1.22+6.85/2 =4.035 The question asks for the nearest hundredth, so round to 4.04.
10. Ans) The mean will have a higher value than the median.
A data set distribution that is skewed right is asymmetrical and has a large number of values at the lower end and few numbers at the high end. In this case, the median, which is the middle number when you sort the data from smallest to largest, lies in the lower range of values (where most of the numbers are). However, because the mean finds the average of all the high and low values, the few outlying data points on the high end cause the mean to increase, making it higher than the median.
11. Ans) The mean will have a lower value than the median.
A data set distribution that is skewed left is asymmetrical and has a large number of values at the high end and few numbers at the low end. In this case, the median, which is the middle number when you sort the data from smallest to largest, lies in the upper range of values (where most of the numbers are). However, because the mean finds the average of all the high and low values, the few outlying data points on the low end cause the mean to decrease, making it lower than the median.
12. Ans) The mean and median will be fairly close together.
When a data set has a symmetrical distribution, the mean and the median are close together because the middle value in the data set, when ordered smallest to largest, resembles the balancing point in the data, which occurs at the average.
13. Ans) median
The median is the middle value of the data points when ordered from smallest to largest. When the data is ordered, it no longer takes into account the values of any of the other data points. This makes it resistant to being influenced by outliers. (In other words, outliers don’t really affect the median.) In contrast, the mean takes every specific data value into account. If the data points contain some outliers that are extreme values to one side, the mean will be pulled toward those outliers.
Reference
Statistics: 1,001 Practice Problems For Dummies
 Plantlet The Blogging Platform of Department of Botany, University of Dhaka
Plantlet The Blogging Platform of Department of Botany, University of Dhaka





I may need your help. I tried many ways but couldn’t solve it, but after reading your article, I think you have a way to help me. I’m looking forward for your reply. Thanks.
Thank you for your sharing. I am worried that I lack creative ideas. It is your article that makes me full of hope. Thank you. But, I have a question, can you help me?