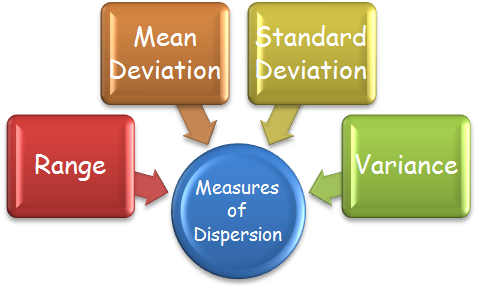
Range
The range consists of a bunch of data that shows the distinction between the highest and lowest values among the data set. So as to seek out the range, it’s necessary to first order the data from lowest to highest. Then we have to subtract the smallest value from the largest value in the set.
Mean deviation
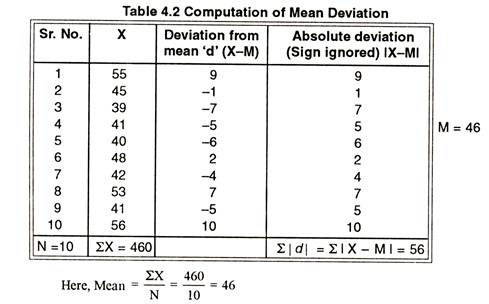
Mean deviation is a statistical measure of the average deviation of values from the mean within a set of samples. It’s calculated by finding the average of the observations. Then the difference of each observation from the mean is decided. The deviations then has got to be averaged. This analysis is mostly used to calculate how sporadic observations are from the mean.
2 5 7 10 12 14
Find out the average of these values by adding them and then and dividing them by the amount of values. In our example, the average is 8.3 (2+5+7+10+12+14=50, which is divided by 6).
Find the difference between each value and the average. Using our example, the differences are: 2 – 8.3 = 6.3 5 – 8.3 = 3.3 7 – 8.3 = 1.3 10 – 8.3 = 1.7 12 – 8.3 = 3.7 14 – 8.3 = 5.7
Find out the average of the differences by adding them and dividing by the number of observations. The average of the differences in this example is 3.66: (6.3+3.3+1.3+1.7+3.7+5.7 divided by 6).Get Free Netflix Now
Best safe and secure cloud storage with password protection
Get Envato Elements, Prime Video, Hotstar and Netflix For Free
Best Money Earning Website 100$ Day
#1 Top ranking article submission website
Variance
Variance is actually the expectation of the squared deviation of a variate from its mean. Informally, variance measures how far a group of numbers are spread out from their average value.
The variance is actually the square of the standard deviation.
*Variance value is usually positive[0 to (+ve)]
Standard Deviation(SD)
In statistics, the standard deviation is a calculation of the amount of variation or dispersion of a group of values. A low standard deviation directs that the values tend to be close to the mean of the set, on the other hand a high standard deviation indicates that the values are spread out over a wider range.
Standard Error(SE)
Whatever be the sampling procedure or the care taken while selecting the sample, the sample estimates of statistics, (X —, s or p) will differ from population parameters (μ, σ or P) because of chance or biological variability. Such a difference between sample and population values is measured by statistic know as sampling error or standard error or (SE).
**Standard error is thus a measure of chance variation and it doesn’t mean error or mistake.
The standard error is the measure of the approximate standard deviation of a statistical sample . The standard error measures the accuracy with which a sample distribution represents a population by using standard deviation. In statistics, a sample mean deviates from the actual mean of a population and this deviation is named the standard error of the mean.
The term “standard error” refers to the standard deviation of various sample statistics, such as the mean or median. For instance, the term “standard error of the mean” refers to the standard deviation of the distribution of sample means taken from a population. The smaller the standard error, the more representative the sample are going to be.
The relationship between the standard error and the standard deviation therefore is , for a given sample size, the standard error equals the standard deviation divided by the square root of the sample size. The standard error is reciprocally proportional to the sample size. The greater the sample size, the smaller the standard error because the statistic will approach the actual value.
- The standard error is the measure which shows the approximate standard deviation of a statistical sample.
- The standard error will consist the variation between the calculated mean of the population and one which is taken into account, or accepted as accurate.
- The more data points involved within the calculations of the mean, the smaller the standard error.
Coefficient of Variation
The coefficient of variation is a statistical measure which shows the dispersion of data points within a data series around the mean. The coefficient of variation represents the ratio of the standard deviation to the mean and it is a useful statistic for comparing the degree of variation from one data series to a different one.
Confidence Interval
A confidence interval refers to the probability that a population parameter will fall between two set values for a certain proportion of times. Confidence intervals measure the degree of uncertainty or certainty in a sampling method and can take any number of probabilities with the foremost common being a 95% or 99% confidence level.
- A confidence interval calculates the likelihood or probability that a population parameter will fall between two set values.
- Confidence intervals calculate the degree of uncertainty or certainty in a sampling method.
- Most of the time, confidence intervals reflect confidence levels of 95% or 99%.
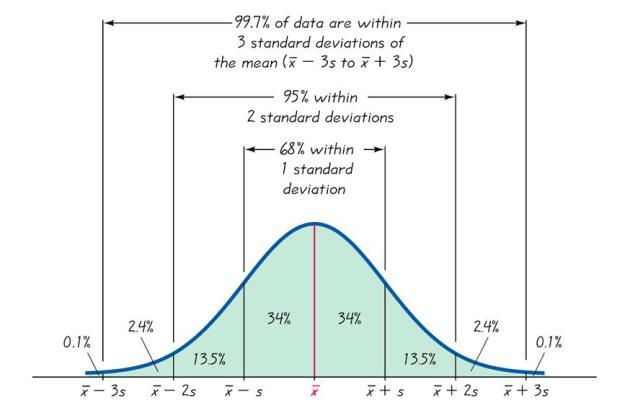
Empirical Rule
The empirical rule conjointly named as the three-sigma rule or the 68-95-99.7 rule provides a quick estimate of the spread of data in a normal distribution given the mean and standard deviation. Specifically the empirical rule indicates that for a normal distribution:
- 68% of the info/data will fall within one standard deviation of the mean.
- 95% of the info/data will fall within two standard deviations of the mean.
- Almost all (99.7%) of the info or data will fall within three standard deviations of the mean.
Q&A
1. What does the standard deviation measure?
2. According to the 68-95-99.7 rule, or the empirical rule, if a data set has a normal distribution, approximately what percentage of data will be within one standard deviation of the mean?
3. A realtor tells you that the average cost of houses in a town is $176,000. You want to know how much the prices of the houses may vary from this average. What measurement do you need?
(A) standard deviation
(B) interquartile range
(C) variance
(D) percentile
(E) Choice (A) or (C)
4. What measure(s) of variation is/are sensitive to outliers?
(A) margin of error
(B) interquartile range
(C) standard deviation
(D) Choices (A) and (B)
(E) Choices (A) and (C)
5. You take a random sample of ten car owners and ask them, “To the nearest year, how old is your current car?” Their responses are as follows: 0 years, 1 year, 2 years, 4 years, 8 years, 3 years, 10 years, 17 years, 2 years, 7 years. To the nearest year, what is the standard deviation of this sample?
6. A sample is taken of the ages in years of 12 people who attend a movie. The results are as follows: 12 years, 10 years, 16 years, 22 years, 24 years, 18 years, 30 years, 32 years, 19 years, 20 years, 35 years, 26 years. To the nearest year, what is the standard deviation for this sample?
7. A large math class takes a midterm exam worth a total of 100 points. Following is a random sample of 20 students’ scores from the class:
Score of 98 points: 2 students
Score of 95 points: 1 student
Score of 92 points: 3 students
Score of 88 points: 4 students
Score of 87 points: 2 students
Score of 85 points: 2 students
Score of 81 points: 1 student
Score of 78 points: 2 students
Score of 73 points: 1 student
Score of 72 points: 1 student
Score of 65 points: 1 student
To the nearest tenth of a point, what is the standard deviation of the exam scores for the students in this sample?
8. A manufacturer of jet engines measures a turbine part to the nearest 0.001 centimeters. A sample of parts has the following data set: 5.001, 5.002, 5.005, 5.000, 5.010, 5.009, 5.003, 5.002, 5.001, 5.000. What is the standard deviation for this sample?
9. Two companies pay their employees the same average salary of $42,000 per year. The salary data in Ace Corp. has a standard deviation of $10,000, whereas Magna Company salary data has a standard deviation of $30,000. What, if anything, does this mean?
10. In which of the following situations would having a small standard deviation be most important?
(A) determining the variation in the wealth of retired people
(B) measuring the variation in circuitry components when manufacturing computer chips
(C) comparing the population of cities in different areas of the country
(D) comparing the amount of time it takes to complete education courses on the Internet
(E) measuring the variation in the production of different varieties of apple trees
11. Everyone at a company is given a year-end bonus of $2,000. How will this affect the standard deviation of the annual salaries in the company that year?
12. Calculate the sample variance and the standard deviation for the following measurements of weights of apples: 7 oz, 6 oz, 5 oz, 6 oz, 9 oz. Express your answers in the proper units of measurement and round to the nearest tenth.
13. Calculate the sample variance and the standard deviation for the following measurements of assembly time required to build an MP3 player: 15 min, 16 min, 18 min, 10 min, 9 min. Express your answers in the proper units of measurement and round to the nearest whole number.
14. Which of the following data sets has the same standard deviation as the data set with the numbers 1, 2, 3, 4, 5? (Do this problem without any calculations!)
(A) Data Set 1: 6, 7, 8, 9, 10
(B) Data Set 2: –2, –1, 0, 1, 2
(C) Data Set 3: 0.1, 0.2, 0.3, 0.4, 0.5
(D) Choices (A) and (B)
(E) None of the data sets gives the same standard deviation as the data set 1, 2, 3, 4, 5.
1. (Ans) how concentrated the data is around the mean
A standard deviation measures the amount of variability among the numbers in a data set. It calculates the typical distance of a data point from the mean of the data. If the standard deviation is relatively large, it means the data is quite spread out away from the mean. If the standard deviation is relatively small, it means the data is concentrated near the mean.
2. ( Ans) approximately 68%
According to the empirical rule, the bell-shaped curve of a normal distribution will have 68% of the data points within one standard deviation of the mean.
3. (Ans) E. Choice (A) or (C) (standard deviation or variance)
The standard deviation is a way of measuring the typical distance that data is from the mean and is in the same units as the original data. The variance is a way of measuring the typical squared distance from the mean and isn’t in the same units as the original data. Both the standard deviation and variance measure variation in the data, but the standard deviation is easier to interpret.
4. (Ans) E. Choices (A) and (C) (margin of error; standard deviation)
The standard deviation measures the typical distance from the data to the mean (using all the data to calculate). Outliers are far from the mean, so the more outliers there are, the higher the standard deviation will be. You calculate the margin of error by using the sample standard deviation so it’s also sensitive to outliers. The interquartile range is the range of the middle 50% of the data, so outliers won’t be included, making it less sensitive to outliers than the standard deviation or margin of error
5. (Ans) 5 years
The formula for the sample standard deviation of a data set is
s=√[∑(x− ̄x)²/ n−1 ]where x is a single value, ̄x is the mean of all the values, represents the sum of the squared differences from the mean, and n is the sample size.
First, find the mean of the data set by adding together the data points and then dividing by the sample size (in this case, n = 10):
̄x =(0+1+2+4+8+3+10+17+2+7) /10
=54 /10
=5.4
Then, subtract the mean from each number in the data set and square the differences, (x – ̄x)²: (0 – 5.4)² = (–5.4)²= 29.16
(1 – 5.4)²= (–4.4)² = 19.36
(2 – 5.4)² = (–3.4)² = 11.56
(4 – 5.4)² = (–1.4)² = 1.96
(8 – 5.4)² = (2.6)² = 6.76
(3 – 5.4)² = (–2.4)² = 5.76
(10 – 5.4)²= (4.6)²= 21.16
(17 – 5.4)² = (11.6)²= 134.56
(2 – 5.4)² = (–3.4)²= 11.56
(7 – 5.4)²= (1.6)² = 2.56
Next, add up the results from the squared differences: 29.16 + 19.36 + 11.56 + 1.96 + 6.76 + 5.76 + 21.16 + 134.56 + 11.56 + 2.56 = 244.4 Finally, plug the numbers into the formula for the sample standard deviation:
s=
√{∑(x− ̄x)2 /n−1} =√(244.4/ 10−1) =√27.156 =5.21 The question asks for the nearest year, so round to 5 years.
6. (Ans) 8 years
The formula for the sample standard deviation of a data set is
s=√{∑(x− ̄x)²/ n−1} where x is a single value, ̄x is the mean of all the values, represents the sum of the squared differences from the mean, and n is the sample size
First, find the mean of the data set by adding together the data points and then
dividing by the sample size (in this case, n = 12):
̄x =(12+10+16+22+24+18+30+32+19+20+35+26)/ 12
=264 /12
=22
Then, subtract the mean from each number in the data set and square the differences, (x – ̄x)2:
(12 – 22)² = (–10)² = 100
(10 – 22)²= (–12)² = 144
(16 – 22)² = (–6)² = 36
(22 – 22)² = (0)² = 0
(24 – 22)² = (2)² = 4
(18 – 22)²= (4)² = 16
(30 – 22)² = (8)²= 64
(32 – 22)² = (10)² = 100
(19 – 22)²= (–3)² = 9
(20 – 22)² = (–2)² = 4
(35 – 22)² = (13)² = 169
(26 – 22)² = (4)² = 16
Next, add up the results from the squared differences: 100 + 144 + 36 + 0 + 4 + 16 + 64 + 100 + 9 + 4 + 169 + 16 = 662 Finally, plug the numbers into the formula for the sample standard deviation:
s=√{∑(x− ̄x)²/ n−1} =√(662 /12−1) =√60.1818 =7.76 The question asks for the nearest year, so round to 8 years.
7. (Ans) 8.7 points
The formula for the sample standard deviation of a data set is
s=√[∑(x− ̄x)²/ n−1 ]where x is a single value, ̄x is the mean of all the values, represents the sum of the squared differences from the mean, and n is the sample size.
First, find the mean of the data set. Although you don’t have a list of all the individual values, you do know the test score for each student in the sample. For example, you know that three students scored 92 points, so if you listed every student’s score individually, you’d see 92 three times, or (92)(3). To find the mean this way, multiply each exam score by the number of students who received that score, add the products together, and then divide by the number of students in the sample (n = 20):
(98)(2) = 196
(95)(1) = 95
(92)(3) = 276
(88)(4) = 352
(87)(2) = 174
(85)(2) = 170
(81)(1) = 81
(78)(2) = 156
(73)(1) = 73
(72)(1) = 72
(65)(1) = 65
̄x =196+95+276+352+174+170+81+156+73+72+65 /20
=1,710/ 20
=85.5
Next, subtract the mean from each different exam score in the data set and square the differences, (x – ̄x)². Note: There are 11 different exam scores here — 98, 95, 92, 88, 87, 85, 81, 78, 73, 72, and 65 — but 20 students. First, work with the 11 exam scores.
(98 – 85.5)2 = (12.5)2 = 156.25
(95 – 85.5)2 = (9.5)2 = 90.25
(92 – 85.5)2 = (6.5)2 = 42.25
(88 – 85.5)2 = (2.5)2 = 6.25
(87 – 85.5)2 = (1.5)2 = 2.25
(85 – 85.5)2 = (–0.5)2 = 0.25
(81 – 85.5)2 = (–4.5)2 = 20.25
(78 – 85.5)2 = (–7.5)2 = 56.25
(73 – 85.5)2 = (–12.5)2 = 156.25
(72 – 85.5)2 = (–13.5)2 = 182.25
(65 – 85.5)2 = (–20.5)2 = 420.25
Now, multiply each value by the number of students who got that score: (156.25)(2) = 312.5
(90.25)(1) = 90.25
(42.25)(3) = 126.75
(6.25)(4) = 25
(2.25)(2) = 4.5
(0.25)(2) = 0.5
(20.25)(1) = 20.25
(56.25)(2) = 112.5
(156.25)(1) = 156.25
(182.25)(1) = 182.25
(420.25)(1) = 420.25
Then, add up those results: 312.5 + 90.25 + 126.75 + 25 + 4.5 + 0.5 + 20.25 + 112.5 + 156.25 + 182.25 + 420.25 = 1,451 Finally, plug the numbers into the formula for the sample standard deviation
s=√{(x-x¯)/n-1}=√(1451/20-1 )=√76.37=8.74
The question asks for the nearest tenth of a point, so round to 8.7.
8. (Ans) 0.0036 cm
The formula for the sample standard deviation of a data set is
s=√[∑(x− ̄x)²/ n−1 ]
where x is a single value, ̄x is the mean of all the values, represents the sum of the squared differences from the mean, and n is the sample size.
First, find the mean of the data set by adding together the data points and then dividing by the sample size (in this case, n = 10):
̄x =(5.001+5.002+5.005+5.010+5.009+5.003+5.002+5.001+5.000)/ 10
=50.033/ 10
=5.0033
Then, subtract the mean from each number in the data set and square the differences, (x – ̄x)²:
(5.001 – 5.0033)² = (–0.0023)² = 0.00000529
(5.002 – 5.0033)² = (–0.0013)² = 0.00000169
(5.005 – 5.0033)² = (0.0017)² = 0.00000289
(5.000 – 5.0033)² = (–0.0033)² = 0.00001089
(5.010 – 5.0033)² = (0.0067)² = 0.00004489
(5.009 – 5.0033)² = (0.0057)² = 0.00003249
(5.003 – 5.0033)² = (–0.0003)² = 0.00000009
(5.002 – 5.0033)² = (–0.0013)² = 0.00000169
(5.001 – 5.0033)² = (–0.0023)² = 0.00000529
(5.000 – 5.0033)² = (–0.0033)² = 0.00001089
Next, add up the results from the squared differences: 0.00000529 + 0.00000169 + 0.00000289 + 0.00001089 + 0.00004489 + 0.00003249 + 0.00000009 + 0.00000169 + 0.00000529 + 0.00001089 = 0.0001161 Finally, plug the numbers into the formula for the sample standard deviation:
s=√{∑(x− ̄x)²/n−1} =√(0.0001161 /10−1 )=√0.0000129 =0.0036 The sample standard deviation for the jet engine turbine part is 0.0036 centimeters.
9. (Ans) There is more variation in salaries in Magna Company than in Ace Corp.
The larger standard deviation in Magna Company shows a greater variation of salaries in both directions from the mean than Ace Corp. The standard deviation measures on average how spread out the data is (for example, the high and low salaries at each company).
10. (Ans) B. measuring the variation in circuitry components when manufacturing computer chips
The quality of the vast majority of manufacturing processes depends on reducing variation to as little as possible. If a manufacturing process has a large standard deviation, it indicates a lack of predictability in the quality and usefulness of the end product.
11. (Ans) There will be no change in the standard deviation.
All the data points will shift up $2,000, and as a result, the mean will also increase by $2,000. But each individual salary’s distance (or deviation) from the mean will be the same, so the standard deviation will stay the same.
12. (Ans) The sample variance is 2.3 ounces². The standard deviation is 1.5 ounces.
You find the sample variance with the following formula: s² = ∑(x− ̄x)²/n−1 where x is a single value, ̄x is the mean of all the values, represents the sum of the squared difference scores, and n is the sample size. First, find the mean by adding together the data points and dividing by the sample size (in this case, n = 5):
̄x =7+6+5+6+9 5
=33 5
=6.6 Then, subtract the mean from each data point and square the differences, (x− ̄x)²:
(7 – 6.6)² = (0.4)² = 0.16
(6 – 6.6)² = (–0.6)² = 0.36
(5 – 6.6)²= (–1.6)² = 2.56
(6 – 6.6)² = (–0.6)² = 0.36
(9 – 6.6)² = (2.4)² = 5.76
Next, plug the numbers into the formula for the sample variance:
The sample variance is 2.3 ounces². But these units don’t make sense because there’s no such thing as “square ounces.” However, the standard deviation is the square root of the variance, so it can then be expressed in the original units: s = 1.5 ounces (rounded). For this reason, standard deviation is preferred over the variance when it comes to measuring and interpreting variability in a data set.
13. (Ans) The sample variance is 15 minutes². The standard deviation is 4 minutes.
The formula for the sample standard deviation of a data set is
s=√[∑(x− ̄x)²/ n−1 ]
where x is a single value, ̄x is the mean of all the values, represents the sum of the squared differences from the mean, and n is the sample size.
First, find the mean by adding together the data points and dividing by the sample size (in this case, n = 5):
̄x =15+16+18+10+9/ 5
=68/ 5
=13.6 Then, subtract the mean from each data point and square the differences, (x− ̄x)2:
(15 – 13.6)2 = (1.4)2 = 1.96
(16 – 13.6)2 = (2.4)2 = 5.76
(18 – 13.6)2 = (4.4)2 = 19.36
(10 – 13.6)2 = (–3.6)2 = 12.96
(9 – 13.6)2 = (–4.6)2 = 21.16
Next, plug the numbers into the formula for the sample variance:
s² = ∑(x− ̄x)²/n−1
=1.96+5.76+19.36+12.96+21.16 /5−1
=61.2/ 4
=15.3
The sample variance is 15.3 minutes². But these units don’t make sense because there’s no such thing as “square minutes.” However, the standard deviation is the square root of the variance, so it can then be expressed in the original units: s = 3.91 minutes (rounded up to 4). For this reason, standard deviation is preferred over the variance when it comes to measuring and interpreting variability in a data set.
14. (Ans) D. Choices (A) and (B) (Data Set 1; Data Set 2)
The original data set contains the numbers 1, 2, 3, 4, 5. Data Set 1 just shifts those numbers up by five units to get 6, 7, 8, 9, 10. Standard deviation represents typical (or average) distance from the mean, and although the mean in Data Set 1 changes from 3 to 8, the distances from each point to that new mean stay the same as they were for the original data set, so the average distance from the mean is the same. Data Set 2 contains the numbers –2, –1, 0, 1, 2. These numbers shift the original data set’s values down by three units. For example, 1 – 3 = –2, 2 – 3 = –1, and so forth. Therefore, the standard deviation doesn’t change from the original data set. Data Set 3 divides all the numbers in the original data set by 10, making them closer to the mean, on average, than the original data set. Therefore, the standard deviation is smaller.
Reference
Statistics: 1,001 Practice Problems For Dummies.
Revised by
- Saifun Nahar Smriti on 16 August, 2020. (This article needs further improvement.)
 Plantlet The Blogging Platform of Department of Botany, University of Dhaka
Plantlet The Blogging Platform of Department of Botany, University of Dhaka