Objectives of this articleTo understand
|
Read the previous article: Introduction to biostatistics part 1
Population
In statistics, a population is a set of homogeneous items or events that is of interest for some question or experiment.
Characteristics
- The population is a huge material.
- A population may be infinite or finite. If a population consists of a specified number of values, it is said to be finite. If the population contains an endless succession of values, the population is an infinite one.
Best safe and secure cloud storage with password protection
Get Envato Elements, Prime Video, Hotstar and Netflix For Free
Best Money Earning Website 100$ Day
#1 Top ranking article submission website
Example: Birth weights of all babies in a particular hospital in month May, the monthly expenditure of non-residential students of 2nd year in Department of Botany, etc.
Sample
A sample is a smaller group of members of a population selected as a representative of the population.
In statistical inference, a subset or a portion of the population (a statistical sample) is chosen to represent the population in statistical analysis. If a sample is chosen properly, characteristics of the complete population that the sample is drawn from can be estimated from corresponding characteristics of the sample.
Characteristics
- The size of the sampling depends on population size.
- It can be defined as a part of a population.
- The method of selecting samples from a population is called Sampling.
- Inference about the population is drawn from studying the sample.
-
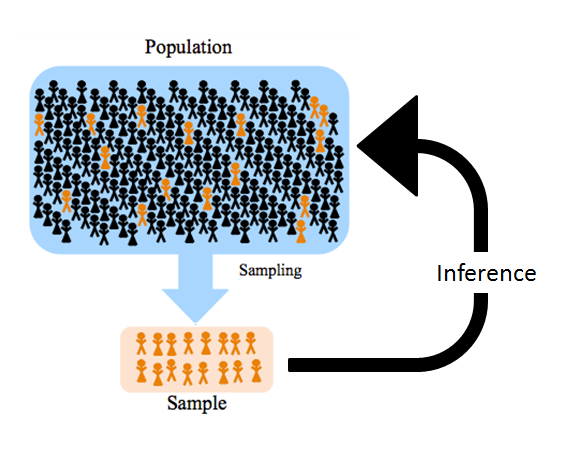
population to sample and vice versa. Source: online.stat.psu.edu

Random Sampling
Selecting samples being unbiased is called random sampling. A very important feature of a good study is that the sample is randomly selected from the target population. Randomly means that every member of the target population has an identical chance of being included in the sample. In other words, the method you use for selecting your sample can not be biased.
It’s important because if you select your subjects in a biased way, then your results will also be biased. And more likely, it wouldn’t represent the population.
Read more about Random Sampling
Understanding Biasness
Suppose you’re making a phone survey on the job satisfaction of Bangladeshis. If you call them at home during the day between 8 a.m. and 5 p.m. you’ll miss out on all those who work or has a job during the day; it could be that day workers are more satisfied than night workers.
Or your boss told you to make a survey of the overall development of the office from the year 2010 to 2020. To make your boss happy while sampling you chose the things as samples that actually developed but didn’t count those which almost remained the same or demoted in 10 years.
Like the above-mentioned examples, there are many ways of being biased. To get a good survey it’s necessary to avoid all kinds of biasness possible.
References
Mahajan BK 2002. (Methods in Biostatistics)(6th edition)
Deborah Rumsey (Statistics for Dummies)
Q&A
You want to calculate the percentage of female versus male shoppers at a department store. So on a Saturday morning, you place data collectors at each of the store’s four entrances for three hours, and you have them record how many men and women enter the store during that time.
1. Why collecting data at the store on one Saturday morning for three hours can cause bias in the data?
- It assumes that Saturday shoppers represent the whole population of people who shop at the store during the week.
- It assumes that the same percentage of female shoppers shop on Saturday mornings as any other time or day of the week.
- Perhaps couples are more likely to shop together on Saturday mornings than during the rest of the week, bringing the percentage of males and females closer than during other times of the week.
- The subjects in the study weren’t selected at random.
- All of these choices are true.
Ans: E. All of these choices are true.
Bias is systematic favoritism in the data. You want to get data that represents all customers at the store, irrespective of what day or what time they shop, whether they shop in couples or alone, and so on. You can’t assume that the people who shopped during those three hours on that Saturday morning are representative of the store’s total clients. This sample wasn’t drawn randomly — everyone who walked in was counted.
Statistic & Parameter
Parameter
Parameter is a summary value that describes the population such as its mean, variance, correlation coefficient, proportion, etc.
- It is a characteristic of a population.
Statistic
Statistic is a summary value that describes the sample as its mean, standard deviation, standard error, correlation coefficient, proportion, etc.
- It is a characteristic of sample.
The value is calculated from the sample and is often applied to the population but may or may not be a valid estimate of the population.

There is a good reason that the population parameter and sample static will vary; hopefully very little but can be significant too if the sample is biased or too small (i.e. doesn’t represent the population properly).
Q&A
You’re assigned to a job where you have to know what percent of all households in a large city has a single woman as the head of the household. To calculate this percentage, you survey 200 households and determine how many of these 200 are headed by a single woman.
1. In this example, what is the population?
2. In this example, what is the sample?
3. In this example, what is the parameter?
4. In this example, what is the statistic?
1. Ans: All households in the city.
A population is a complete or whole group you’re interested in studying. The aim here is to estimate what percent of all households in a large city has a single woman as the head of the household. The population is total households and the variable is whether a single woman runs the household.
2. Ans: Selected 200 households.
The sample is a portion or subset drawn from the entire population you’re interested in studying. In this inference, the sample is the 200 households selected out of all the households in the city.
3. Ans: The percent of households headed by single women in the city.
A parameter is some characteristic of the population. Because studying a population directly isn’t generally possible, parameters are usually estimated by using statistics (numbers calculated from sample data).
4. Ans: The percent of households headed by single women within the 200 selected households.
A statistic is a number representing some characteristic that you calculate from your sample data; the statistic is used to estimate the parameter (the same characteristic in the population).
Reference
Statistics: 1,001 Practice Problems For Dummies
 Plantlet The Blogging Platform of Department of Botany, University of Dhaka
Plantlet The Blogging Platform of Department of Botany, University of Dhaka






This was ”easy to understand” type of article. Hope to see more like this.
Thanks a lot for your precious feedback.
Reading your article has greatly helped me, and I agree with you. But I still have some questions. Can you help me? I will pay attention to your answer. thank you.