Thermodynamics: A Relationships Between Heat and Other Forms of Energy (Part 1)

The study of the flow of warmth or the other sort of energy into or out of a system because it undergoes a physical or chemical transformation, is named Thermodynamics. In other word relationship between heat, work, temperature, and energy. In broad terms, thermodynamics deals with the transfer of energy from one place to a different and from one form to a different . The key concept is that heat may be a sort of energy like a particular amount of mechanical work.

Get Free Netflix Now

Best safe and secure cloud storage with password protection

GPL Themes For Free

Get Envato Elements, Prime Video, Hotstar and Netflix For Free

Best Money Earning Website 100$ Day

Best ever Chat Forum

#1 Top ranking article submission website

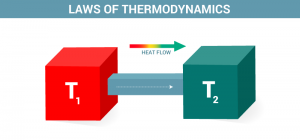
Examples of Thermodynamics

The increase within the energy of the green matter is adequate to the decrease within the energy of the environment . Photosynthesis can thus be treated as a thermodynamic process, where energy transfers from the biosphere to plants and vegetation. a big amount of free energy is lost within the complex biochemical pathways between the absorption of sunshine and therefore the output of carbohydrate; it’s possible that these losses could also be considered during a general thermodynamic manner.

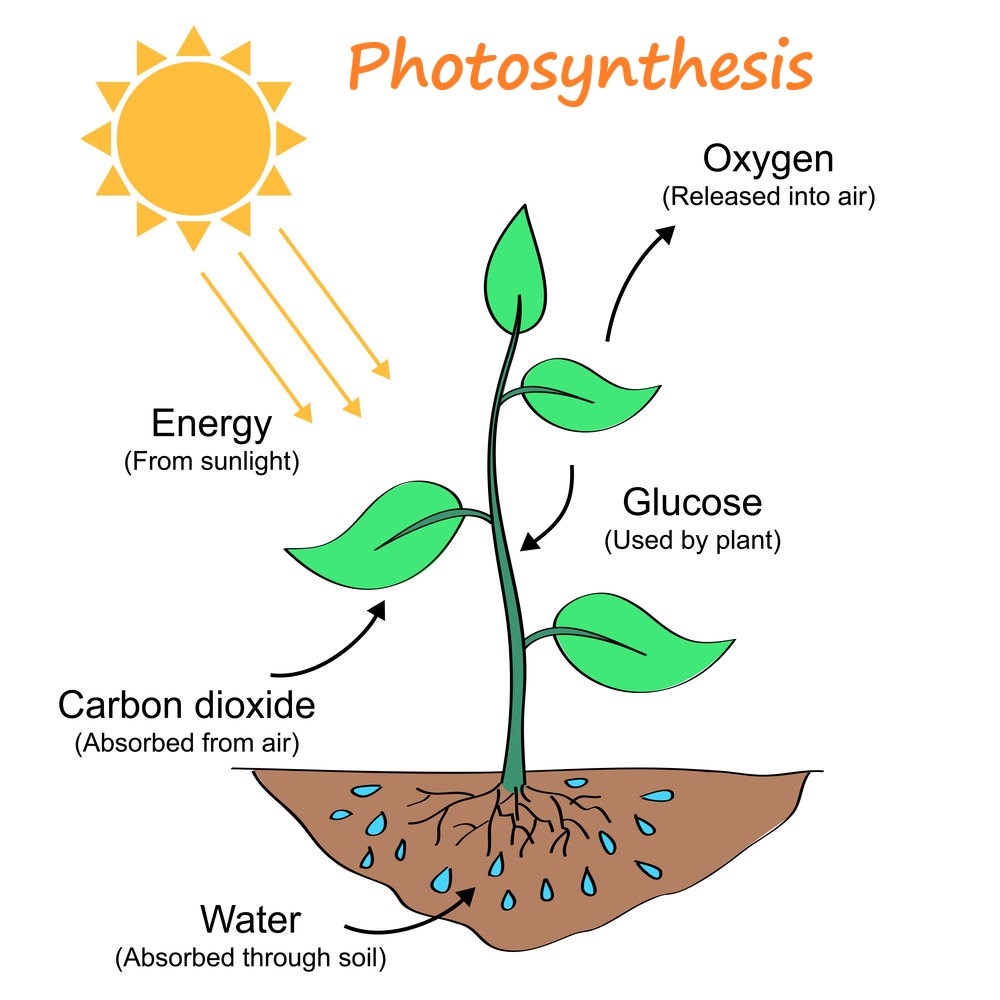
Thermodynamics of photosynthesis has been a topic of interest to the scientific community; it’s , therefore, addressed during this paper. This work reveals that traditional thermodynamic relationships could also be wont to calculate and project photosynthesis. solar power is required for the reaction of green matter production. When the dimensions of the green matter expands, less solar power is received by the environment and more energy is stored in plants and vegetation. If everything else is that the same, the rise within the energy produced is adequate to the decrease within the heat of the biosphere and the other way around . Photosynthesis expansion is thus like heat transfer from the biosphere to the green matter. Plants surrounding air could also be assumed as a heat reservoir at air dry bulb temperature, Tdb. The colder air enclosed by the space of the green matter could also be assumed as a chilly reservoir at air wet bulb temperature, Twb, and photosynthesis could also be represented by a Carnot engine cycle. The thermal efficiency of the cycle is adequate to 1-(Twb/Tdb)0.5. If everything else is that the same, the difference, Tdb-Twb, may be a limiting factor of terrestrial photosynthesis. supported this understanding, equations to predict growth of the green matter and tree diameter are derived and validated supported observations. Other findings include photosynthesis global average thermal efficiency is between 0.61% and 0.72%, and seasonal greening is almost 0.80%. Neglecting deforestation, surface greening trend with global climate change is between 0.23% and 0.28% annually.

Thermodynamic Terms and Basic Concepts

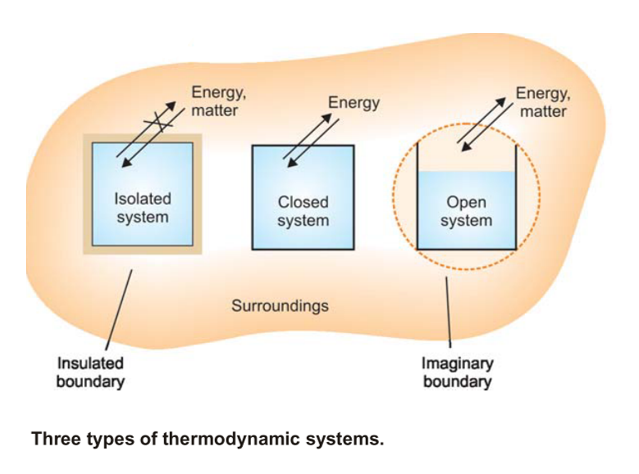
• In studying and evaluating the flow of energy into or out of a system, it will be useful to consider changes in certain properties of the system.
• These properties include temperature, pressure, volume and concentration of the system.
• Measuring the changes in these properties from the initial state to the final state, can provide information concerning changes in energy and related quantities such as heat and work.

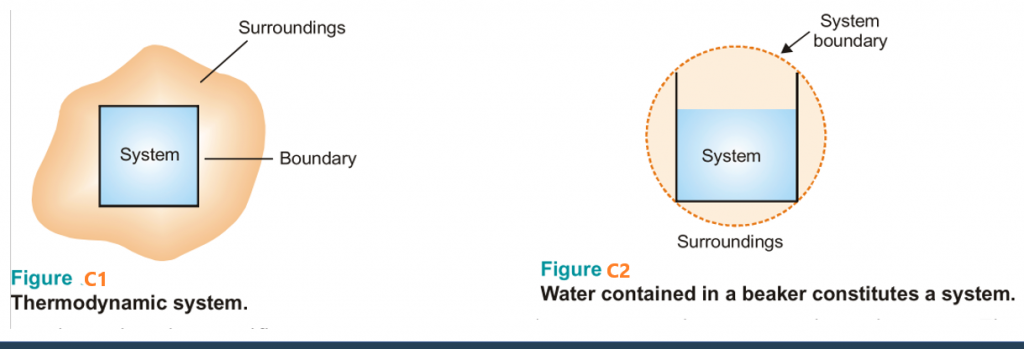
• A system is that part of the universe which is under thermodynamic study and the rest of the universe is surroundings.
• The real or imaginary surface separating the system from the surroundings is called the boundary.

Intensive and Extensive Properties of a System

• Intensive Properties: A property which does not depend on the quantity of matter present in the system, is known as Intensive Property. Examples: pressure, temperature, density, and concentration.
• Extensive Properties: A property that does depend on the quantity of matter present in the system, is called an Extensive Property. Examples: volume, number of moles, enthalpy, entropy, and Gibbs’ free energy.

STATE OF A SYSTEM

• A thermodynamic system is said to be in a certain state when all its properties are fixed. The fundamental properties which determine the state of a system are pressure (P), temperature (T), volume (V), mass and composition.
• Since a change in the magnitude of such properties alters the state of the system, these are referred to as State variables or State functions or Thermodynamic parameters.

Equilibrium and Non-Equilibrium States

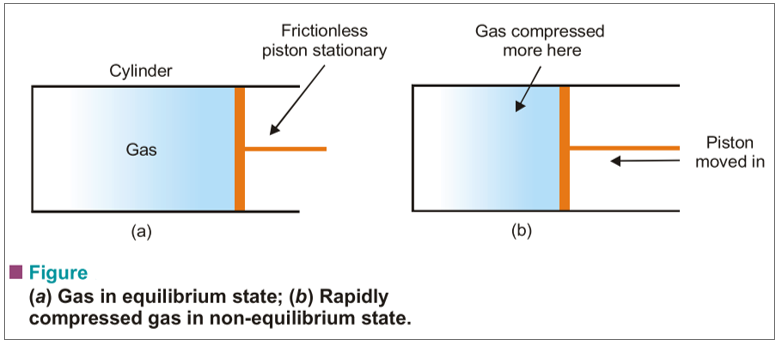
A system during which the state variables have constant values throughout the system is claimed to be during a state of thermodynamic equilibrium. Suppose we’ve a gas confined during a cylinder that features a frictionless piston. If the piston is stationary, the state of the gas are often specified by giving the values of pressure and volume. The system is then during a state of equilibrium.

A system during which the state variables have different values in several parts of the system is claimed to be during a non-equilibrium state. If the gas contained during a cylinder, as stated above, is compressed very rapidly by moving down the piston, it passes through states during which pressure and temperature can not be specified, since these properties vary throughout the gas. The gas then would be said to be in non-equilibrium state.

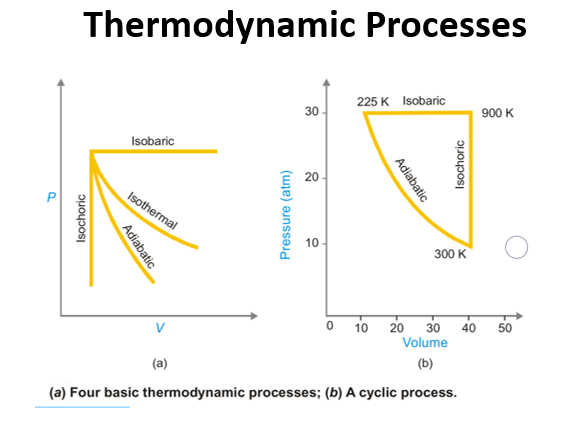
Thermodynamic Processes

• When a thermodynamic system changes from one state to another, the operation is called a Process.
• These processes involve the change of conditions (temperature, pressure and volume).
• The various types of thermodynamic processes are:

1. Isothermal Processes: Those processes in which the temperature remains fixed, are termed isothermal processes. This is often achieved by placing the system in a thermostat (a constant temperature bath). For an isothermal process dT = 0
2.  Adiabatic Processes: Those processes in which no heat can flow into or out of the system, are called adiabatic processes.

• Adiabatic conditions can be approached by carrying the process in an insulated container such as ‘thermos’ bottle.
• For an adiabatic process dq = 0

First Law of Thermodynamics

Law of Conservation of Energy to the thermodynamic system:

• ‘The total energy of an isolated system remains constant, though it may change from one form to another’.
• When a system is changed from state A to state B, it undergoes a change in the internal energy from EA to EB.
• Thus, we can write ΔE = EB – EA.
• This energy change is brought about by the evolution or absorption of heat and/or by work being done by the system.
• Because the total energy of the system must remain constant, we can write the mathematical statement of the First Law as:
•               ΔE = q – w ……….(1)
• Where q = the amount of heat supplied to the system, w = work done by the system
• Thus First Law may also be stated as : the net energy change of a closed system is equal to the heat transferred to the system minus the work done by the system.
• To illustrate the mathematical statement of the First Law, let us consider the system ‘expanding hot gas’ (Fig. K).

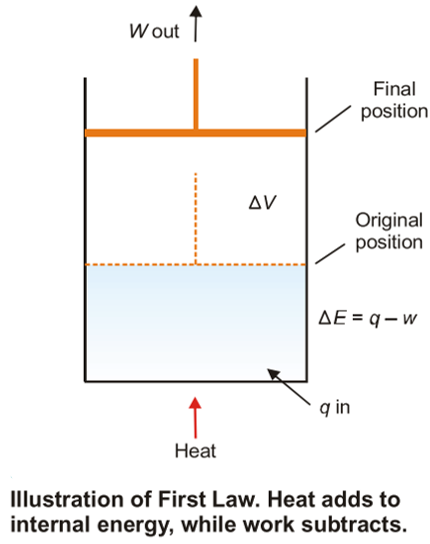
• The gas expands against an applied constant pressure by volume ΔV.
• The total mechanical work done is given by the relation:
•                          w = P × ΔV …(2)
• From (1) and (2), we can restate:
•       ΔE = q – P × ΔV

Check out the other part of this article in Thermodynamics: Part 2.(Click Here)

Reference

This Article is based on by the lecture of Dr. Md. Ismail Hosen,

Assistant Professor, Department of Biochemistry and Molecular Biology

University of Dhaka.

 Some info and pictures have been added by Author and from Wikipedia.

Reference used for info: Cambridge International AS and A Level Physics Coursebook.