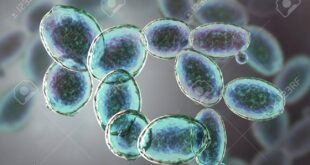
The phylum Ascomycota (colloquially called ascomycetes) is by far the largest group of fungi, estimated to include more than 32000 described species in 3400 genera (Kirk et al., 2001). It is assumed that the majority of ascomycetes has yet to be discovered, and the total number of species may well be higher by a factor of 10-20 or even more (see Hawksworth, 2001).
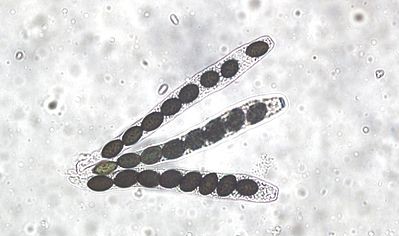
The name is derived from the Greek words askos (a leather bottle, bag or bladder) and mykes (a fungus), so ascomycetes are sac fungi. The characteristic feature of the group is that the sexually produced spores, the ascospores, are contained within a sac, the ascus. In most ascomycetes the ascus contains eight ascospores and is turgid, ejecting its spores by a squirt mechanism.
The ascus forming yeasts, some of the common black molds and green molds, the powdery mildews, the cup fungi, the morels, and the truffles are among the best known examples of Ascomycetes.
Good to know
In the fungi, karyogamy occurs immediately or very soon after plasmogamy, yet in the subdivisions Ascomycotina and Basidiomycotina, a short-lived (in Ascomycotina) or long-lived (in Basidiomycotina) dikaryotic stage is interspersed between plasmogamy and karyogamy.
The Ascomycetes and the Basidiomycetes are sometimes called “higher fungi.” They are considerably more complex in structure than the fungi we have studied in Lower Fungi section (Actinomycetes, Chytridiomycetes, Oomycetes & Zygomycetes).
Occurrence
Ascomycetes can be found in a variety of habitats and at most seasons of the year. Many are small and inconspicuous, parasitic on plants, and evident only from the effects they produce on their hosts. Others are saprobic, live on the soil or on decaying logs and leaf mold, and produce large, easily discernible fruiting bodies. A few are entirely hypogean (Gr. hypo = under + ge = earth), developing and remaining underground. A number of Ascomycetes are coprophilous (Gr. kopros = dung + philein = to love), growing only on the dung of certain animals.
General Characteristics
The one character distinguishing the Ascomycetes from all other fungi is the ascus (pi. asci, Gr. askos = goat skin, sac), a sac-like cell containing a usually definite number of ascospores (Gr. askos + spora = seed, spore) formed by free cell formation after karyogamy and meiosis. Eight ascospores are typically formed within the ascus, but this number may vary from one to over a thousand according to the species.
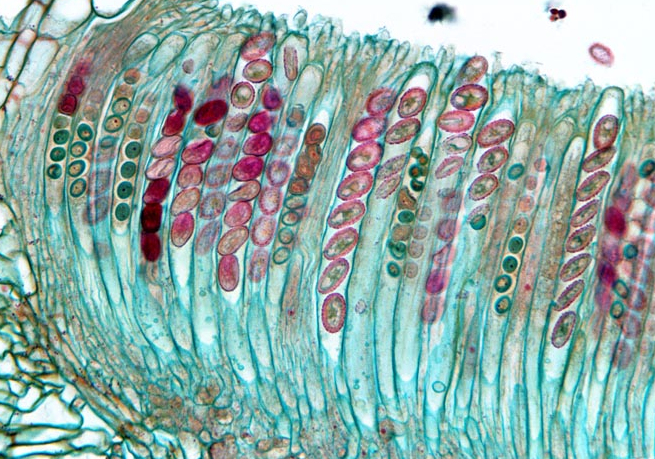
Other characteristics of the Ascomycetes are a septate mycelium, the production by most species of a fruiting body enclosing the asci, and the complete absence of any type of flagellate cell. These, however, are secondary characteristics that occur in other fungi as well.
If a fungus produces its spores in asci, it is an ascomycete regardless of any other character; if it does not, it may not be properly placed in this class.
The Ascomycetes in general have two distinct reproductive phases: the ascus or sexual stage, often called the ascigerous or perfect stage, and the conidial or asexual stage, often designated as the imperfect stage.
Since ascomycete classification is based primarily on the characteristics of the perfect stage, such forms do not present a problem to the systematist.
Relation between Ascomycetes & Deuteromycetes: A very large number of fungi exist that are known only by their conidial stages (asexual). Since these imperfect stages are similar to those of known Ascomycetes, it is almost certain that many of the so called imperfect fungi (Deuteromycetes) are actually Ascomycetes that have either lost their ascus stages as a result of their evolutionary development, or possess ascus stages as yet undiscovered. In either case, this large group of imperfect Ascomycetes constitutes one of the greatest taxonomic problems of the mycologist.
Somatic Structure
The mycelium of the Ascomycetes is composed of septate hyphae, the walls of which contain a large proportion of chitin. The hyphae are well developed, slender or stout and profusely branched.
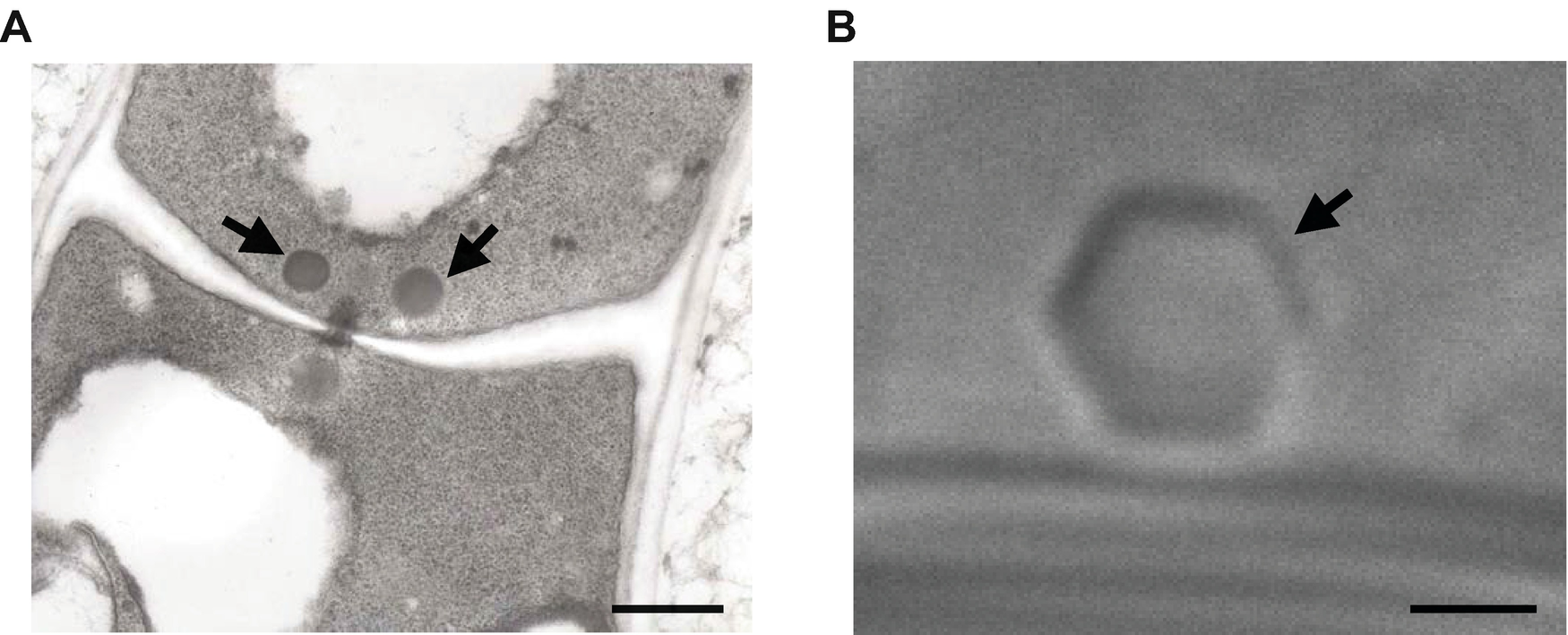
The formation of a septum in hyphae begins at the hyphal periphery and advances toward the center, thus invaginating the plasma membrane. But to maintain the cytoplasmic connection between cells, the septum protruding inwards from lateral wall to not meet in the middle, thus creating a septal pore.
Sometimes, the septal pore might be blocked by some proteinaceous organelles termed Woronin bodies (Buller, 1933). The are globose structures or ‘hexagonal’ (polyhedral) crystals made up essentially of one protein (Tenney et al., 2000), and surrounded by a unit membrane. They measure 150-500 nm in width and are sufficiently large to block the septal pore. They rapidly do so near regions where a hypha is physically damaged. Usually one Woronin body blocks one pore. The blockage in the septal pore is also consolidated by deposition of further material (for references see Markham & Collinge, 1987; Markham, 1994)
The cells are often uninucleate, but mycelia consisting of multinucleate cells are also quite common. If the mycelium originates from the germination of a single, uninucleate spore, the mycelium will be homokaryotic. Heterokaryotic mycelium may originate in a variety of ways.
Fungal Tissues
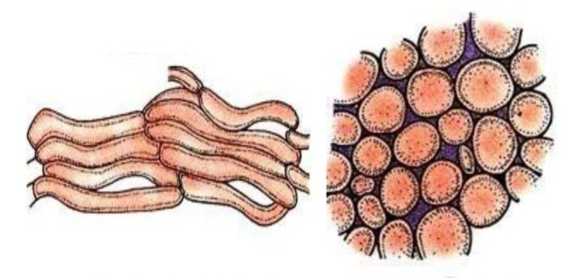
Ascomycete mycelium is often organized into fungal tissues (plectenchyma). If such a tissue is loosely woven and the mycelial strands are more or less evident, it is known as prosenchyma. If, however, the tissue is closely woven, if the hyphae have lost their individuality, if the cells are more or less isodiametric, and if the tissue in general resembles the parenchyma of plants, it is known as pseudoparenchyma.
Not all Ascomycetes possess mycelium. For example, some yeasts are unicellular; others produce a chain of cells that form a false mycelium (pseudomycelium); still others are unicellular under certain conditions, but mycelial under others. This condition is known as dimorphism and is known to occur in the Ascomycetes and their close relatives the Deuteromycetes as well as in the Zygomycetes,
Best safe and secure cloud storage with password protection
Get Envato Elements, Prime Video, Hotstar and Netflix For Free
Best Money Earning Website 100$ Day
#1 Top ranking article submission website
Importance of Ascomycetous Fungi
Harmful Aspects
The Ascomycetes are of great importance in human affairs. The cellulolytic Ascomycetes, such as Chaetomium. are among the organisms responsible for the destruction of fabrics containing cellulose. In destroying crops and crop plants as well as timber and ornamental trees, the Ascomycetes are among our worst fungous enemies, causing such diseases as apple scab, brown rot of stone fruits, powdery mildews, foot rot of cereals, ear rot of corn, and many others.

The chestnut blight, caused by the ascomycete Endothia parasitica, has almost completely annihilated the chestnut forests of America, and the Dutch elm disease, caused by another ascomycete, Ceratocystis ulmi, threatens the American elm with extinction.
Some diseases of our domestic animals and of humans are of ascomycetous origin; histoplasmosis, a respiratory disease, is one example; body ringworm, another. Of interest in this connection is the ergot fungus, Claviceps purpurea, an ascomycete whose mycelium invades and destroys the ovaries of the rye plant and other grasses, thus causing a plant disease and in so doing producing sclerotia with alkaloids that are deadly to animals and human beings if consumed, but, properly administered, very important as medicinal drugs.
Beneficial Aspects
Many Ascomycetes are beneficial. The fermenting activities of certain yeasts are the basis of the baking and brewing industries. The morels and truffles also enjoy a fame of special importance among the fungi, for discriminating eaters consider them second to none in delicacy of flavor.
Besides, if we include in the Ascomycetes those imperfect fungi (Deuteromycetes) that probably have ascomycetous affinities, the Ascomycetes become of tremendous importance indeed.
Related Articles
References
- Buller, A. H. R. & Vanterpool, T. C. (1933). The violent discharge of the basidiospores (secondary conidia) of Tilletia tritici. In A. H. R. Buller, Researches on Fungi, 5, pp. 207-278. London: Longmans, Green & Co.
- Hawksworth, D. L. (2001). The magnitude of fungal diversity: the 1.5 million species estimate revisited. Mycological Research, 105, 1422-1432
- Introduction to Fungi (3rd edition) by John Webster & Roland W. S. Weber.
- Introductory Mycology by C. J. Alexopoulos & C. W. Mims.
- Kirk, P. M., Cannon, P. F., David, J. C. & Stalpers, J. A., eds. (2001). Dictionary of the Fungi, 9th edn. Wallingford, UK: CABI Publishing.
- Markham, P. (1994). Occlusions of the septal pores of filamentous fungi. Mycological Research, 98, 1089-1106.
- Markham, P. & Collinge, A. J. (1987). Woronin bodies of filamentous fungi. FEMS Microbiology Reviews, 46, 1-11.
- Tenney, K., Hunt, I., Sweigard, J., et al. (2000). hex-1, a gene unique to filamentous fungi, encodes the major protein of the Woronin body and functions as a plug for septal pores. Fungal Genetics and Biology, 31, 205-217.
- The Fifth Kingdom: An Introduction to Mycology (4th edition) by Bryce Kendrick.
 Plantlet The Blogging Platform of Department of Botany, University of Dhaka
Plantlet The Blogging Platform of Department of Botany, University of Dhaka